Graph Theory — Max_Min Flow
Advanced Graph Theory — Maximum Flow

If you often wonder how a Network Flow takes place in a network or how to detemine maximum flow of information from a source to its destination, then this blog would satisfy all your curiosities.
This blog describes a flow network and contains some primary definitions for better understanding of the flow network. It also describes the Ford-Fulkerson Algorithm, a popular algorithm for calculating Max-Flow in a network.
Prerequisites:
- Breadth First Search
- Basic Graph Theory concepts.
What is a Flow Network ?
In graph theory, a flow network is defined as a directed graph involving a source(S) and a sink or a target(T) and several other nodes connected with edges.
Every edge in a flow network has a capacity associated with it. Capacity of a flow network is defined as the maximum limit of flow that is possible along a given edge.
It is easy to visualize a flow network as a network of water pipes, the capacity here means the maximum amount of water that can flow through a particular pipe per second.It is obvious that the rate of flow of water along a pipe would never exceed its capacity.
A residual capacity of an directed edge is the capacity minus the flow.
An augmenting path is simple path in the residual graph, i.e. along the edges whose residual capacity is positive.
What are the properties of a Flow Network?
- For any node, except the source and the target node, Input Flow = Output Flow.
- The flow of an edge cannot exceed its capacity i.e.0 ≤ f(e) ≤ c(e).
- Total flow out of the source node is equal to the total flow in the sink node.
- Net flow in the edges follows skew symmetry i.e. f((v,u)) = — f((u,v)).
What is Maximum Flow?
It is defined as the maximum amount of flow that the network would allow from source to sink.
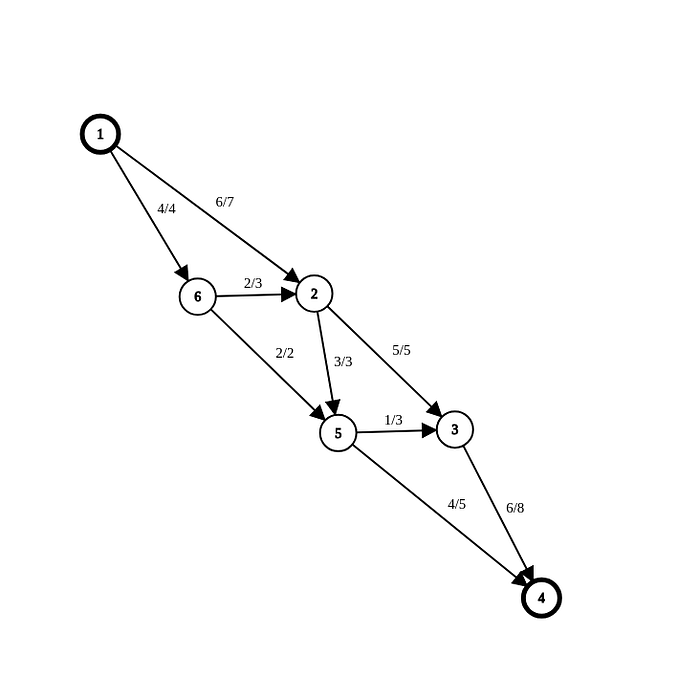
There are several algorithms to find maximum flow in a network. One of the simplest algo is the Ford-Fulkerson Algorithm.
function: FordFulkerson(Graph G,Node S,Node T):
Initialise flow in all edges to 0
while (there exists an augmenting path(P) between S and T in residual network graph):
Augment flow between S to T along the path P
Update residual network graph
returnThe Ford-Fulkerson method works as follows. First we set the flow of each edge to zero. Then we look for an augmenting path from sto t. An augmenting path is a simple path in the residual graph, i.e. along the edges whose residual capacity is positive. If such a path is found, then we can increase the flow along these edges.
We keep on searching for augmenting paths and increasing the flow. Once there doesn’t exists an augmenting path any more, the flow is maximal.
Let us specify in more detail, what increasing the flow along an augmenting path means. Let C be the smallest residual capacity of the edges in the path. Then we increase the flow in the following way: we update f((u,v)) += Cf((u,v)) += C and f((v,u)) -= Cf((v,u)) -= C for every edge (u,v) in the path.
Edmonds-Karp algorithm: -
It is an implementation of the Ford-Fulkerson method that uses BFS for finding augmenting paths
Implementation
- Time Complexity — O(VE²), where V is the number of vertices and E, the number of edges.
Extra Gyaan :
- Integral Flow Theorem — This theorem states that if every capacity in the network is integer, then the flow in each edge will be integer in the maximal flow.
- Max-flow min-cut theorem — This theorem states that in a flow network, the maximum amount of flow passing from the source to the sink is equal to the total weight of the edges in the minimum cut, i.e. the smallest total weight of the edges which if removed would disconnect the source from the sink.

Some Practice Problems on Max-Flow:
Happy Coding!!
